跳到主要内容

模拟赛题解/2025.9.1 模拟赛

· 阅读需 9 分钟
Sintle
Sintle
Developer

T1-序（ryvius）​

题面​

对于一个长度为 nn 的正整数数列 aa，aa 是好的当且仅当对任意 1≤i<n,ai≠ai+11\leq i<n,a_i\not=a_{i+1}。

现在有一个好的数列 aa，可以对这个数列执行以下操作：

  • 选择一个位置 i(1≤i≤n)i(1\leq i\leq n) 和一个正整数 xx，将 aia_i 变为 xx，需要保证每次操作后这个序列都是好的。

要让整个序列操作完之后只有两种不同的数值，求至少要操作多少次。

1≤T≤105,1≤n≤2×105,2≤∑n≤2×105,1≤ai≤n1\leq T\leq10^5,1\leq n\leq2\times10^5,2\leq \sum n\leq 2\times10^5,1\leq a_i\leq n。

题解​

考虑到序列的最终形态是两个数 a,ba,b 交替出现，于是将序列按位分为奇偶两部分。

考虑对于两个数，将序列调整到对应状态的最小次数，显然由两个部分组成：

  • 序列中不满足最终形态的数的数量
  • 存在这两个数相邻的情况数量

于是考虑枚举偶数位并统计奇数位贡献，对于不存在第二种情况的数对，可以直接选择出现次数最多的奇数位，显然此时结果最小。

对于存在第二种情况的数对，因为这样的数对显然不超过 O(n)O(n) 个，因此可以用 map 维护，直接枚举。

复杂度 O(nlog⁡n)O(n\log n)。

T2-破（kon）​

题面​

放学后茶会的几人决定去毕业旅行！但是她们关于该去哪里旅行有一点小分歧，所以她们决定用阿弥陀签来抽签决定目的地。话虽这么说，但是 Yui 希望操纵抽签结果， 所以她来找你帮忙了！

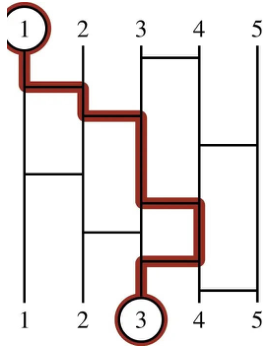
上面是一个简化版的阿弥陀签的示例。一个阿弥陀签由 nn 条编号为 1∼n1\sim n 的竖线和若于条高度互不相同的横线构成，每条横线在某个高度上连接相邻的两条竖线。简单来说，使用阿弥陀签抽签的流程如下：

  1. 首先，选择一条竖线，将其最上端（高度最小的一端）作为起点；
  2. 然后，从起点开始向下走，每次碰到一条横线的一端，都必须走到其另一端再继续向下走。
  3. 这次抽签的结果就是到最下端时所在竖线的编号。

现在，Mio 正在制作一个阿弥陀签。目前签上已经画好了 nn 条竖线，还没有任何横线，接下来她将在这个阿弥陀签上修改 qq 次横线。每一次她会在某一个位置增加或者减少一条横线。Yui 在每次操作之后，想知道修改后的整个阿弥陀签至少删掉多少条横线，才能使得对于 ∀1≤i≤n\forall 1\leq i\leq n，以第 ii 条竖线的最上端作为起点时，到达最下端时也在第 ii 条竖线。你能帮帮她吗？

1≤x1,x2≤n≤20,1≤h,q≤2×105,1≤y≤h,∣x1−x2∣=11\leq x_1,x_2\leq n\leq 20,1\leq h,q\leq 2\times10^5,1\leq y\leq h,|x_1-x_2|=1。

题解​

可以将这个过程转化为有 nn 个人分别从不同的起点开始走，每条横线视作将相邻的两个人交换，则我们的目标是使最终所有人回到原先的位置。

设每个人最后的位置为 pip_i，则每次修改可以视为交换两个 pip_i，最终的目标则转化为令 ∀1≤i≤n,pi=i\forall 1\leq i\leq n,p_i=i。

注意到对于所有 pi≠ip_i\not=i，必定存在 k(k≤n)k(k\leq n) 个置换环，而每个置换环都需要 li−1l_i-1 次删除操作（即删除其中一次置换对应的横线）来满足最终条件，因此最终的删除边数量就是 n−kn-k。

所以我们只需要开一棵线段树维护置换环数量即可。

T3-Q（tamako）​

题面​

在一个 n×nn\times n 的方格纸上的某些格子有障碍，使得剩下的所有格子可以用 1×21\times 2 的多米诺骨牌不重叠地填满。

将要在方格纸上额外选两个格子放置障碍，使得不再能用骨牌填满所有空格。有多少种选择两个格子的方案。

如果方案数超过 10610^6，你需要输出 10610^6 而非方案数。

1≤n,m≤10001\leq n,m\leq 1000。

题解​

假设空格数量为 xx，对整个方格纸进行黑白间隔染色，那么会有 x2\frac{x}{2} 个黑空格和 x2\frac{x}{2} 个白空格。由于删除两个同色格子一定会导致方格纸无法再用多米诺骨牌填满，我们至少有 x2(x2−1)\frac{x}{2}(\frac{x}{2}-1) 种方案，所以 x>2000x>2000 时一定输出 10000001000000。

考虑 x≤2000x\leq2000 的情况。我们可以把输入中的所有空格当成点建一张二分图，两个点之间连无向边当且仅当它们对应的空格在方格纸上相邻。显然这个图一定存在一个完美匹配，我们先把这个匹配找出来。然后我们考虑数有多少个点对满足删完之后仍然存在完美匹配。

对于一对异侧点 (u,v)(u,v) 而言，假设它们在原图中分别匹配上了 u′,v′u',v'，删除这对点之后是否仍然存在完美匹配可以这样判断：我们先取消 u,vu,v 在原图中的匹配，然后删掉这两个点，检查 u′→v′u'\rightarrow v' 是否是一条合法的增广路。具体来说就是，是否存在一条从 u′u' 到 v′v' 的路径 (u′,p1,p2,p3,⋯ ,pk,v′)(u',p_1,p_2,p_3,\cdots,p_k,v')，满足 (p1,p2),(p3,p4),⋯ ,(pk−1,pk)(p_1,p_2),(p_3,p_4),\cdots,(p_k−1,p_k) 都是原图中的匹配。我们枚举所有的 u′u'，从 u′u' 开始 bfs 所有可行的 v′v' 即可。

记答案上限为 R=106R=10^6，那么时间复杂度是 O(R)O(R) 的。

T4-终（hotel）​

题面​

有一个由 A 和 S 构成的字符串。

这群史莱姆会进行以下四种操作：

  1. A 进行分裂：在一个 A 的两端各增加一个 S。即将字符串中的某个 A 替换为 SAS。
  2. S 进行分裂：在一个 S 的两端各增加一个 A。即将字符串中的某个 S 替换为 ASA。
  3. A 组团逃跑：连续 aa 个 A 可以消失。即删除字符串中的连续 个 A。
  4. S 组团逃跑：连续 ss 个 S 可以消失。即删除字符串中的连续 个 S。

给出两个常数 aa 和 ss，有两个字符串 R1R_1 和 R2R_2，求是否能将 R1R_1 经过若干次操作转换为 R2R_2。

1≤T≤100,1≤a,s≤109,1≤∣R1∣,∣R2∣≤501\leq T\leq100,1\leq a,s\leq10^9,1\leq|R_1|,|R_2|\leq50。

题解​

记 ε\varepsilon 表示空串，RkR^k 表示字符串 RR 重复 kk 次。

经过足够的手玩，我们可以发现：

ASA→AaSAa→SASA\rightarrow A^aSA^a\rightarrow S，同理 SAS→ASAS\rightarrow A。

AA→ASAS→SSAA\rightarrow ASAS\rightarrow SS，同理 SS→AASS\rightarrow AA。

SA→SSAS→AAAS→ASSSSA\rightarrow SSAS\rightarrow AAAS\rightarrow ASSS，同理 AS→SAAAAS\rightarrow SAAA。

A→SAS→AAASS→ASSSSA\rightarrow SAS\rightarrow AAASS\rightarrow ASSSS，同理 S→SAAAAS\rightarrow SAAAA。

A→ASSSS→AAAAAA\rightarrow ASSSS\rightarrow AAAAA，同理 S→SSSSSS\rightarrow SSSSS。

所以，我们可以在一个非空串的任何位置添加 A4A^4 和 S4S^4。也就是说：

ε→A4\varepsilon\rightarrow A^4，同理，ε→S4\varepsilon\rightarrow S^4。

ε→A4a→Aa\varepsilon\rightarrow A^{4a}\rightarrow A^a，同理 ε→Ss\varepsilon\rightarrow S^s。

就是说，所有操作都是可逆的，那么：

ε↔Aa↔A4↔Agcd⁡(a,4)↔Sgcd⁡(s,4)\varepsilon\leftrightarrow Aa\leftrightarrow A4\leftrightarrow A\gcd (a,4)\leftrightarrow S \gcd (s,4)。 显然答案只与 gcd⁡(a,4)\gcd(a,4) 和 gcd⁡(s,4)\gcd(s,4) 有关，所以下面只考虑 a∣4a|4 且 s∣4s|4 的情况。不妨设 a ∣ s ∣ 4a\,|\,s\,|\,4。

对于任意的 aa，ss 和字符串 RR，我们考虑以下对字符串 RR 的操作：

  1. 首先，假如 R 中存在子串 SA，将其替换为 ASSS，直到所有 S 都在 A 右侧为 止。
  2. 随后，消去所有连续的 A4 和 S 4。
  3. 随后，如果有至少两个 S，将最前面的 SS 替换为 AA。如果有 A4 就消去。

显然，经过这样的操作后，R 一定是以下八个串之一：

ε,A,AA,AAA,S,AS,AAS,AAAS\varepsilon,A,AA,AAA,S,AS,AAS,AAAS。我们将这些串称作标准串。

当然，ε\varepsilon 之后并不能进 行任何操作，你可以把它当成 A4A^4，这并不重要。

那么，我们只需要考虑分类讨论一下，在不同的 aa 和 ss 下，这八个串之间哪些能互相转移即可。

对于 a=s=4a=s=4 的情况，这八个串之间并不能互相转移。证明也很简单：显然最后得到的串只跟上述第二步操作结束之后的字符串中，AA 和 SS 的个数 mod  4\mod4 的值有关。 题目中的操作 1,3,41,3,4 不会改变这两者的值，而操作 22 会使得这两者同时 +2+2。无论如何都不会改变最终的结果。

a=s=1a=s=1 是平凡的。

a=1,s>1a=1,s>1 时，相当于所有的 AA 都不存在，那么 SSSS 也不存在。此时只有 ε\varepsilon 和 SS 两种情况。

a=2a=2 时，AAAA 和 SSSS 仍然不存在。有 ε,A,S,AS\varepsilon,A,S,AS 四种情况。由于 2∣a2|a 时 AA 的数量的奇偶性不会改变，所以这些情况下所有情况之间不能转移是显然的。

所以，我们只需要求出 R1R_1 和 R2R_2 对应的标准串，并看它们能否互相转移即可。

时间复杂度 O(∣R1∣+∣R2∣)O(|R1|+|R2|)。